豆寄席第46回『エンジニアにとっての現代数学を考える - 道具箱の中のツールとしての数学の勧め』開催報告

2026年01月21日イベント報告

嶺山　良介

本稿は、豆寄席第46回の開催報告です。

開催概要

タイトル	エンジニアにとっての現代数学を考える - 道具箱の中のtoolとしての数学の勧め
講演者	松谷茂樹氏（金沢大学大学院自然科学研究科教授）
開催日時	2025年9月26日 (金) 18時30分～20時00分
講演概要	技術が目まぐるしく変化・変容する時代、如何に survive するかは各企業、各個人が問われている課題であり、10・20年の先を見据えて如何に技術を積み上げてゆくのかは各技術者に問われている課題です。新規技術が5年後・10年後先にAIやアプリに代替されてゆく状況下で、AIに取って代わられない技能として、数学は一つの重要な候補です。スティーヴンキングは著書『書くことについて』の中でプロフェッショナルのライターは各自固有の道具箱(Toolbox)を持つことを勧めています。どんな状況下においても何時でも、何時でも何処でも使用可能な道具（各自固有の表現方法・用語・執筆テクニック）が入った道具箱です。このような道具箱を持つことは、すべての職業人に対しても言えることです。技術の引出しをたくさん持つことでもあります。技術者の道具箱のツールの一つとして数学を加え、それに磨きをかけると数学は流行に左右されず、時代を超えた強力な武器となります。

講演の流れ

自己紹介
日本の産業界への危機意識
キヤノン時代の数学
企業とアカデミアの差異
二宮忠八から学ぶこと・スティーヴン・キングから学ぶこと
数学の活用方法の要
現場での数学活用のノウハウ
まとめ

1. 自己紹介

松谷氏は、静岡大学で素粒子論の修士号を取得後、キヤノン株式会社に27年間在籍されました。特筆すべきは、企業に在籍しながら土日や通勤時間を利用して数学の研究を続け、博士号（理学）を取得された「パラレルキャリア」です。企業では数理工学研究室の室長として、新規デバイス・新規材料の数理解析などに携わる傍ら、完全に独立した個人研究として、DNAの形状記述に端を発する純粋数学（代数幾何学）や統計力学の探求に進まれました。
この産業界とアカデミア、技術者と純粋数学者という二つの軸で研究を続けられた経験が、氏を「脳の中に純粋数学者が住む技術者」というユニークな人材たらしめ、本講演の独自の視座の源泉となっています。

2. 日本の産業界への危機意識

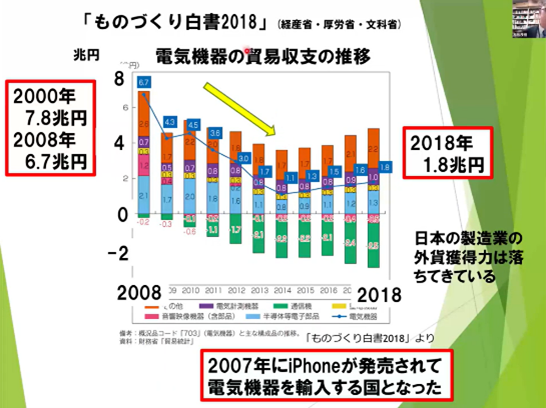
次に、松谷氏は現代日本の製造業が直面している構造的課題について述べられました。氏は経済産業省の「ものづくり白書」のデータを引用し、日本の「電気・情報通信機械工業」分野の貿易収支が、2007年のiPhone登場を境に急激に悪化している現状を指摘。これは、原材料を輸入し、付加価値をつけて製品を輸出するという従来の「加工貿易」モデルが崩壊したことを意味します。

現在の産業構造は、日本のメーカーが優れた部品を作っても、OSやサービス基盤といった「プラットフォーム」を海外企業（プラットフォーマー）に押さえられ、その上で価格競争を強いられる「コモディティ化」（汎用品化）が進んだ結果であると分析されました。
この産業構造の危機に対し、松谷氏は以下の2つの戦略的選択肢を提示しました。

自らがプラットフォーマーを目指す
コモディティ化に対抗し、さらなる技術の先鋭化を図る

その上で、「どちらの道に進むにせよ、数学が重要になる」と述べられました。なぜなら、プラットフォームを構築するにも、精緻なものづくりを行うにも、対象を深く理解し、モデル化し、予測・制御するための数学的思考が不可欠だからです（この点は後述のセクション6で詳しく論じられます）。松谷氏は、この課題に対し、キヤノンで実践してきたアプローチに解決策のヒントがあることを示します。

3. キャノン時代の数学

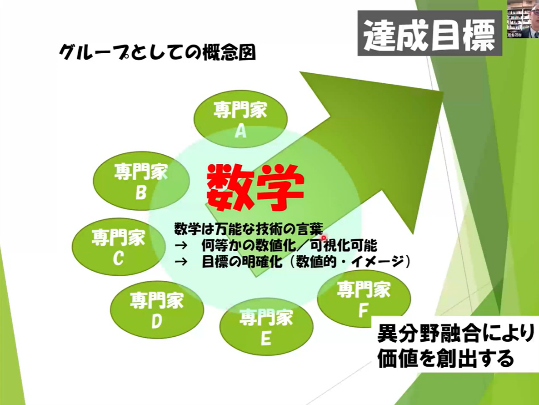
本セクションでは、数学の戦略的価値が、数学単独で成果を出すことにあるのではなく、背景の異なる分野の専門家を結びつける言葉としての役割を果たすことにある、と述べられました。
松谷氏が在籍した数理工学研究部のミッションは、「市販のシミュレーションツールでは解けない問題を、物理現象を数学によって表現することで予測・制御可能にする」ことでした。数理工学研究部ではこのミッションに対して様々な分野の専門家で構成されたチームで取り組んでおり、その中で数学は「万能な技術の言葉」として重要な役割を果たしたといいます。現実世界の現象を数学の言葉に翻訳することによって、数値シミュレーションなどで詳細に定量化・可視化することが可能になり、異なる専門家間の議論や意思統一、方向性の決定ができるようになります。

さらに、現実の世界を数学の言葉に翻訳して考察することによって新たな現実を創造できる時代になっていると松谷氏は続けます。その具体例として、氏のかかわった二つのプロジェクトが紹介されました。インクジェットプリンタ開発では、インク滴の複雑な挙動を予測する際、表面張力が急激に変化する点を捉える必要がありました。松谷氏のチームは「特異点論」（関数の滑らかさが失われる点の構造を研究する幾何学の一分野）を応用し、従来の試行錯誤から数理モデルによる制御へと転換しました。また、材料開発ではフラクタル幾何学（図形の一部を拡大すると元の図形全体と似た形が現れるような複雑な図形を扱う幾何学）を活用し、製品の耐久性向上に貢献しました。このように企業においても新しい成果を生むために現代数学は大きく寄与していることがわかります。また、その一方で現実を数学で用いて深く考察するには従来のユークリッド幾何学や微積分などの初等的な数学だけでは対応できない場合もあります。松谷氏は企業において数理を用いるための勘所として以下のようにまとめを述べられました。

数学は現象を記述・表現できる良いツールである
記述するためにはどのような（高度なものでも初等的なものでも）数学でもOK
対象とする現象に最適の数学を探し出すこと。もし適切な数学が現存しないなら創り出すこと

4. 企業とアカデミアの差異

このような数学の異分野融合における役割を理解する上で、まずアカデミアと企業の研究スタイルの根本的な違いを認識することが重要です。
松谷氏は、科学哲学者トーマス・クーンの「パラダイム」（ある時代の科学者コミュニティに共通する思考の枠組み）の概念を引用し、アカデミアが「専門家集団の内向きの合意」によって発展する「タコ壺化」した構造を持つことを解説しました。各専門分野は、それぞれが独自の言語、評価基準（ピアレビュー＝専門家による査読）、そして解決すべき固有の重要課題を共有しており、分野間のコミュニケーションが困難（専門用語では「通約不可能性がある」と呼ばれる状態）であると指摘しました。
一方、企業活動の本質は、ノーベル賞受賞者である島津製作所の田中耕一氏の「イノベーションに天才は不要、異分野融合の場こそ重要」という言葉に集約されます。企業は、ある製品開発や問題解決という明確な目標達成のために、化学、物理、電気、ソフトウェアといった異なる専門家が集まり、協力して価値を創出する「異分野融合の場」なのです。

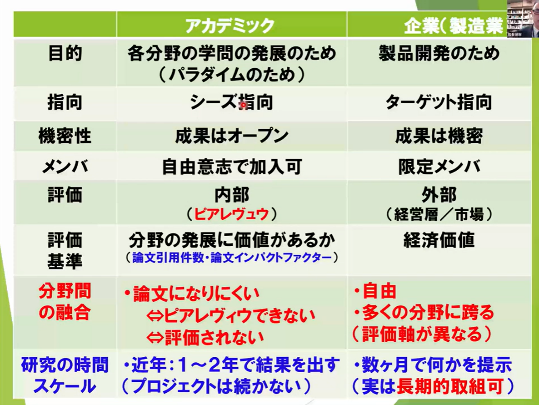
この分析に基づき、松谷氏は「企業側が主体性を持ち、アカデミアが持つ尖った知識や各分野の情報を『ツール』としてうまく活用すべきである」と提言しました。

5. 二宮忠八とスティーヴン・キングから学ぶ「道具箱」の思想

松谷氏は、異なる分野の二人の人物を例に挙げ、エンジニアが持つべき姿勢を説きました。

二宮忠八:
ライト兄弟より早く飛行原理を着想しながらも、「西洋でも聞いたことがない」と支援を断られ、先を越された事例。この教訓から、真に斬新なアイデアは、他人が理解できるプロトタイプが完成するまで「孤独を恐れず独力でやる」気概が重要であると述べました。
スティーヴン・キング:
キングの著書『書くことについて』から、「ものを書くとき、自分の力を最大限に発揮するためには、自分専用の道具箱をつくって、それを持ち運ぶだけの筋肉を鍛えることである。そうすれば、なにがあっても、あわてふためくことなく、いつでもしかるべき道具を手にとって、ただちに仕事にとりかかれる」という言葉を引用。講演参加者の方々もそれぞれ道具箱を持っているはずだと述べ、この講演における提案として、その道具箱に数学を加えてみてはどうか、と呼びかけられました。

AI（人工知能）がどれほど進化しても、数学という道具は古びることがないのです。

6. 数学を「道具」として活用する思考法

このセクションでは、数学的思考のプロセスが哲学的な側面から解説され、エンジニアが習得すべき思考のループが示されました。

STEP 1: 抽象化の認識
「りんご3個とぶどう2房とマスカット1粒で果物は合計何個？」という問いを例に、私たちは日常的に、個性や価値の異なる現実の対象（例：越前蟹3万円と渡り蟹3千円）を、目的（カニの総数を数える）に応じて「同じ1個」として数えるという、高度な「抽象化（捨象）」（特定の性質を抜き出して他を捨てること）を行っていると指摘。この「何を同一と見なすか」という行為の難しさを自覚することが第一歩となります。

STEP 2: 抽象化による問題解決（つるかめ算の例）
「つるかめ算」では、鶴や亀の具体的なイメージから離れ、「x, y」という記号に置き換える（抽象化する）ことで、問題は単純な連立方程式となり、本質的な構造が可視化され、容易に解けるようになります。

STEP 3: 抽象化は哲学的な問題である
哲学者フッサールの「幾何学は測量技術者の言葉を極限操作したもの」という言葉を紹介。日常的な「太い線」から「太さゼロの線」という概念を生み出し、x^2+y^2=1 という数式で「円」を定義する。デカルトは、このような抽象化・理想化をさらに進め、物理世界では無意味な「体積＋面積＋長さ」のような計算が有効に機能する、デカルト座標における代数という新たな世界を創造しました。
このような抽象化・理想化のプロセスにより、人間は現実の物理的制約から解放され、純粋に数学のルールの中で考察を進める道が開かれました。この思考プロセスをまとめると、
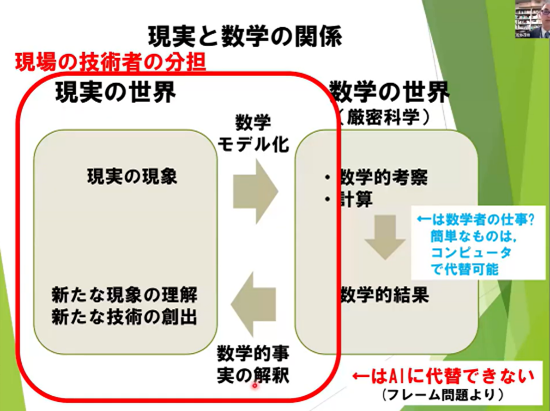
「現実世界 → 数学モデル化 → 数学的考察 → 現実への解釈（フィードバック）」
というループとして捉えることができます。松谷氏は、人間の担う、最も重要でAIには代替できない2つの役割を示しました。
(1) 数学モデル化：現実の複雑な現象から本質を抜き出し、適切な数学の言葉に翻訳する
(2) 結果の解釈：数学が出した答えを現実世界に照らして意味を見出し、次のアクションに繋げる
これらは、「フレーム問題」（AIが自ら問題の枠組みを設定できないこと）と呼ばれ、AIには解決するのが難しい部分であり、人間のもつ創造性が発揮される領域なのです。数学を活用することとは、公式を利用することではない、デカルトのように自分の頭で、自分の言葉で対象を記述することであると述べられました。場合によっては自分で新たな言葉を創りだす必要があります。

7. 現場での数学活用のノウハウ

ではこのような思考プロセスをどうやって実践すればよいでしょうか。講演の最後に数学の活用ノウハウが紹介されました。

どのくらいのレベルで「数学」を活用するかはケース・バイ・ケース
問題や各自の判断に応じて最適な数学を選べばよく、時には高校数学が有効な場合もあります。
規範や模範はない！（How to本は怪しい）
問題によって自分の基準を作って対処する必要があります。よく知られた問題でない限り、「世の中に正解を知っている人がいる」とは思わないほうがよく、自分のなかの自然観などが試されていると考えなければなりません。そのとき、対象とする問題の系（システム全体）を知り抜けば答えは一つに収れんされるであろう、と主張されました。

これらを実践する上で特に重要だと強調されたのはセクション6でも述べられた数学による問題のモデル化です。問題の対象を如何に認識し、それを何でもって表現すべきかは、対象それぞれによって決めるべきことです。手法やスタイルを先に決めて取り組むのではなく、対象に耳をそばだてて、対象の声を聞く必要がある、と主張されました。具体的な事例が2点紹介されました。
実践例1：風景画の表現

松谷氏は、風景の写真を提示し、これを表現する最適な方法は何かと問いかけました。ある風景は写実的な絵画が適し、ある風景は鉛筆によるスケッチが適し、またある風景（富士山）は水墨画のような大胆な抽象化が最も本質を捉えているかもしれない、と述べました。これは、エンジニアが現実の現象をモデル化する際に、「どの数学（どの表現方法）を選ぶか」という対象の認識そのものが重要であることを示唆しています。
実践例2：「コンウェイの法則」の数理モデル化

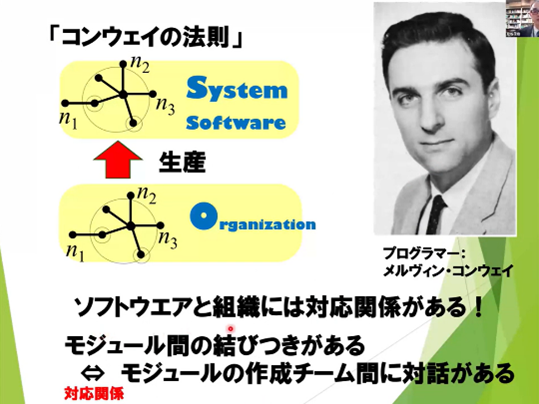
ソフトウェア開発における「コンウェイの法則」（組織構造がシステム設計を規定する）を例に挙げ、これもまた数学的な構造（グラフ構造）として記述できることが示されました。松谷氏が（豆蔵の羽生田栄一氏を含む）共著で発表された論文『コンウェイの法則、数学的視点からのリバイズド』が紹介され、組織やコミュニケーションといった現実の問題も数学の「言葉」で記述可能であることが示されました。

8. まとめ

最後に、本講演全体のまとめとして、以下の点が示されました。

企業とアカデミアの根本的な差異、アカデミアの弱点を理解しながら企業が主体となってアカデミアの知見を利用することが肝要です。
数学は「どうなっているか？」を記述するよいツールであり、論理的な思考ツールです。
現場での数学活用には、現場の視点で言葉としての数学を活用し、現場を知っている技術者が自分で考えること、そして問題を解くよりも作ることが重要であると強調されました。

これらを踏まえ、（普遍的なツールである）数学をあなたの道具箱に加えてみませんか、というメッセージで締めくくられました。

所感

本講演で最も印象的だったのは、松谷氏が示した「対象に耳をそばだて、対象の声を聞く」という姿勢でした。特異点論やフラクタル幾何学といった抽象的な数学も、インク滴の挙動予測や材料の耐久性向上という適切な問題設定の中で扱われることで、鮮明な現実的意味を持ち始める。この「適切な問題設定」こそが、現実をどの数学で記述するかという「モデル化」と、得られた結果を現実に引き戻す「解釈」という、AIには代替できない人間の創造的な営みだと感じました。数学をツールとして道具箱に加えることで、技術の潮流に左右されない思考基盤を築きながら、現実の問題に主体的に向き合う力を養えるのではないかと思います。

今後の 豆寄席 へのご参加もお待ちしております！